The Beauty and Utility of Simple Problems
When we recognize the battle against chaos, mess, and unmastered complexity as one of Computer Science’s major callings, we must admit that “Beauty is our Business.” — Edsger Wybe Dijkstra
As a field of scientific inquiry, Computing Science is unique in its scope and interconnectedness with other disciplines. This breadth however often makes it difficult for faculty to form a coherent narrative, making the curriculum seem like an archipelago of unrelated subjects in the eyes of students1. There are however deep relationships between the various subjects that comprise most computing science curricula, the knowledge of which not only enables us to reason with greater clarity about the artifacts we create, but also provides a coherent narrative under which we can better know our place within the scientific tradition.
In this essay, I present two problems that while seemingly simple, provide a gateway for exploring very diverse and deep questions that are at the core of our discipline: recognizing integers, and the concordance problem.
Recognizing Integers
Programming is the art of refinement of specification. — Niklaus Wirth
Define a function $f$ which satisfies the following claim: If $x$ is a string, then $f(x)$ is true if and only if $x$ represents an integer.
The formulation is deceptively simple, and appears to be precise. Many students, and even industry veterans2 will fairly quickly write something along the following lines:
public static boolean f(String x) {
for (char c : x) {
if (!Character.isDigit(c)) {
return false;
}
}
return true;
}
A cursory read however shows the function wanting. Consider for example the following questions:
- What is the value of $f(\text{’-1’})$?
- What is the value of $f(\text{’+1’})$?
- What is the value of $f(\text{‘0x5A9’})$?
- What is the value of $f(\text{’three’})$?
In each case, the value returned is $\text{false}$. For some of them, this is clearly incorrect. For others however, there are conflicting intuitions. This last part is important, because it illustrates that while something may appear to be precise, that’s not necessarily the case. This is precisely what makes this such a useful interview question - it quickly separates out individuals who gloss over the imprecision of the problem statement from those who stop to ask: “What do you mean when you say that a string represents an integer?”
Now, as they say, “we’re cooking with gas.” Before we can even begin to define the function, we have to more precisely specify what the set of integers we are interested in actually looks like. This now raises a profoundly important question: “How can we go about doing this?” One answer, affords us the opportunity to introduce the concept of finite automata by presenting the notion of an NFA (non-deterministic finite automaton) as means for precisely defining this set:

Figure 1
An NFA defining the set of integers to identify.
Now, the non-determinism of the NFA is problematic on some level if we wish to jump straight to an implementation. This raises another important question: “Can we refine our NFA into some other structure which is more amenable to representation in a program text?” Automata theory tells us that we in fact can convert the NFA into an equivalent DFA (deterministic finite automaton).
The DFA is a remarkable mathematical object which does two things for us. Firstly, it provides a precise definition for the set of integers we are interested in (as does the NFA). This enables us to reformulate the original specification as follows:
Define a function $f$ which satisfies the following claim: If $x$ is a string, then $f(x)$ is true if and only if $x$ is accepted by the deterministic finite automaton shown in Figure 2.
Secondly, its structure tells us the algorithm to use when defining our function $f$ (along with its pertinent properties).

Figure 2
The DFA obtained from Figure 1.
public static boolean f(String x) {
State state = S0;
for (char c : x) {
switch (state) {
case S0:
if (isNonZeroDigit(c)) {
state = S2;
} else if (isUnaryOperator(c)) {
state = S1;
} else if (c == '0') {
state = S3;
}
break;
case S1:
if (isNonZeroDigit(c)) {
state = S2;
} else {
state = E;
}
break;
case S2:
if (!isDigit(c)) {
state = E;
}
break;
case S3:
state = E;
break;
case E:
break;
}
}
return (state == State.S3) ||
(state == State.S2);
}
Approaching the problem in this manner yields a program which has a number of important (and useful) properties:
- Its correctness with respect to specification can be shown rather easily.
- It possesses a high degree of elaboration tolerance3.
- Its performance is better than that of many built-in libraries.
- It is highly amenable to automatic generation.
If we take some time to dwell on what we have accomplished, we can note that we defined a function which given an object $x$, determines whether or not it belongs to a set $S$. Not only that, but $S$ is infinite, and yet we were able to not only describe it in a finite way, but also use our description to derive an efficient algorithm for answering the original question. This is what we mean by software engineering4 - the application of scientific principles to the design of software.
From the perspective of computing science pedagogy, this problem also affords us a way to seamlessly introduce a number of foundational questions in Computing Science:
- What kinds of infinite sets are there?
- Are all of them representable in a finite way? If so how?
- What kinds of infinite sets can we answer the membership question about, and how effectively?
- What can our answers to these questions tell us about our own nature?
The search for answers to these question informed the work of early pioneers such as Turing, Church and others, and connects us to an intellectual tradition reaching back to Pythagoras. Another beautiful aspect of this problem and its solution is that it ties together multiple courses in a Computing Science curriculum, as well as those that are found within the traditional Liberal Arts.
The Concordance Problem
The art of programming is the art of organizing complexity. — Edsger Wybe Dijkstra
A concordance is an alphabetical index of the principal words in a book or the works of an author with their immediate contexts. Concordances are used in many diverse disciplines, but perhaps most famously they are used in the study of the Bible. They can be quite complex in their structure depending on how refined they are in terms of the data they collect. Figure 3 for example, shows a beautiful visualization, generated by Professor Chris Harrison, of all 63,779 cross references that are found in the King James Bible.
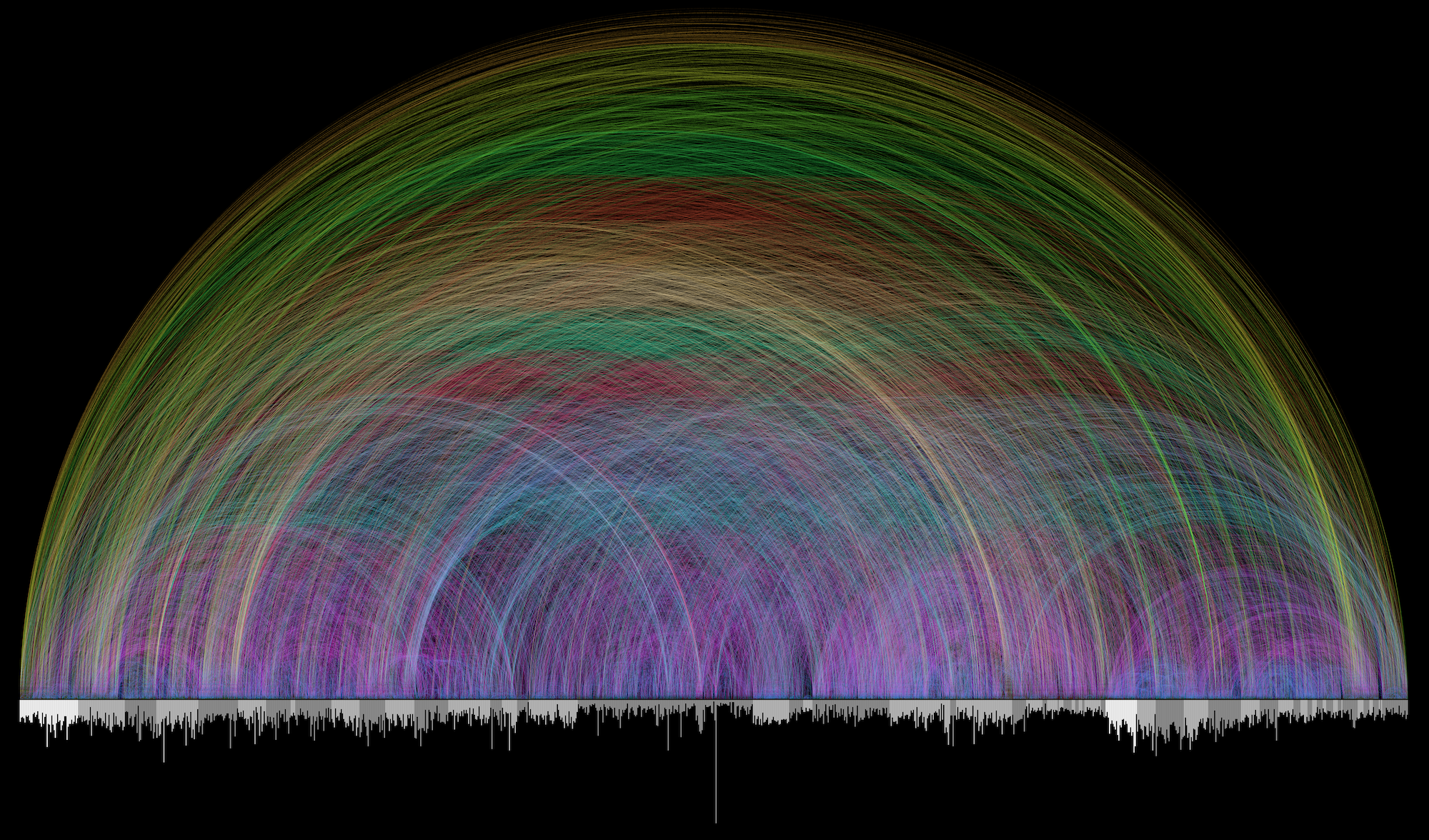
Figure 3
A visualization of all of the cross references in the King James Bible.
This visualization was made famous in a lecture series on the Bible by the renowned psychologist Dr. Jordan Peterson. In the YouTube lecture embedded below, he discusses (among other things) how the Bible can be considered “the first hyperlinked book”:
In addition, there is a strong argument to be made that the large language models (such as GPT-4), which are used for what’s been called generative AI, can be viewed as immensely complex concordances, in which the contextual information for each entry is comprised of billions of pieces of information.
In the context of a programming exercise, a simplified form of the problem of generating a concordance for a given text can be specified as follows:
Define a function $g$ which satisfies the following claim: If $\tau$ is a text, then $g(\tau)$ is a table which associates every word $\omega$ in $\tau$ with the total number of times $\omega$ appears, as well as the line numbers on which it appears.
As with the task of recognizing integers, the specification raises a number of questions, the answers to which have dramatic ramifications for our ultimate solution:
- What do we mean by a text?
- What do we mean by a word?
- What do we mean by a line and a line number?
- What do we mean by a table?
After some time has been spent refining the specification, we can come to the view that a text, word, and line are kinds of sequences. Which raises the question: “What is a sequence and how can we represent one?”
Traditionally, the notion of a sequence is first introduced through the array data structure:

Figure 4
An array of characters.
Across most imperative programming languages, the notation for indexing into an array is fairly standard. Something interesting happens though when you replace the square brackets with parentheses:
This trivial notational shift demonstrates that an array may be viewed as a kind of function:
This shift in perspective affords us the opportunity to discuss several important topics:
- The idea that the distinction between data and algorithms is not always necessary.
- A framework for reasoning about and understanding the set, sequence, and map abstract data types.
- How the relevant topics in a discrete mathematics course tie in to data structures and their analysis.
- How to judge if a particular function ought to be represented as data as opposed to algorithmically.
With regards to potential solutions to the concordance problem, we now have a framework by which we can develop and reason about the following candidate implementation:
private static Concordance generateConcordanceFromFile(String fileName)
throws IOException {
Map<String, SortedSet<Integer>> data = new HashMap<>();
BufferedReader input = new BufferedReader(new FileReader(fileName));
String line;
int lineNumber = 0;
while ((line = input.readLine()) != null) {
lineNumber++;
String[] words = line.toLowerCase().split(DELIMITERS);
for (String word : words) {
if (!word.isEmpty()) {
if (data.containsKey(word)) {
data.get(word).add(lineNumber);
} else {
SortedSet<Integer> lineNumbers = new TreeSet<>();
lineNumbers.add(lineNumber);
data.put(word, lineNumbers);
}
}
}
}
input.close();
return new Concordance(fileName, data);
}
As with the previous problem of recognizing integers, when we take the time to develop a mental model for precisely formulating the problem and reasoning about its design, we can define a solution whose whose correctness can be shown rather easily5, and which possesses a high degree of elaboration tolerance.
Wrapping it Up
Both of the problems presented here illustrate how seemingly simple problems, which are often only quickly touched on in the course of a single lecture on programming, can serve as platforms for connecting together multiple subjects within a Computing Science curriculum. Not only that, but they also open up the ability to tie in subjects ranging from the limitations of human nature (e.g., ramifications of Gödel’s incompleteness theorem or the halting problem), to the interconnectedness of archetypes in religious and mythological texts (e.g., the potential of language models and concordances to illustrate cross-cultural connections in stories). This connects Computing Science as a discipline to the more traditional Liberal Arts, providing us with a myriad of opportunities to introduce our students to a world they typically don’t believe themselves to be a part of.
-
Something which has been exacerbated in Computer Science departments by the rising prevalence and influence of specialists in “computer science education”. ↩︎
-
During my time as a developer at eBay I gave this problem during a technical interview. The gentleman (a 20-year veteran of the software industry) was unable to solve the problem because he got hung up on which software library he was allowed to “import”. ↩︎
-
The term elaboration tolerance was coined by the late John McCarthy, in a paper originally presented in 1998 (an updated variant of which can be found here.) A program is said to be elaboration tolerant if small changes to the specification only require small changes to the implementation. ↩︎
-
This view of software engineering is not without some controversy. “Modern” definitions of the term tend to revolve around certain business and project management concerns. In this essay I am deliberately trying to reclaim the term. ↩︎
-
In fact in many cases when we take the time to think through a problem in this manner we can develop the program in tandem with an informal proof of its correctness. ↩︎